Dominique Duquet
Entre la multitud de números conocidos, hay dos, en particular, a los que podríamos dar el calificativo de “herméticos” o “mistéricos” porque son portadores del misterio y nos permiten el acceso a otra dimensión de la realidad.
Estos números han fascinado a la humanidad desde la noche de los tiempos y todavía continúan atrayendo a los estudiosos en la búsqueda de resoluciones algebraicas o geométricas, a los matemáticos, a los científicos y a los filósofos. El primero de estos números (el número Pi) nos conecta con lo absoluto, y el segundo (el Número de Oro) con lo infinitamente grande o pequeño.
Aunque nos hemos acostumbrado en el lenguaje cotidiano a utilizar el término «número» para nombrarlos a uno u otro, en realidad, lo que vamos a tratar es de «calificar» una cierta relación o proporción, una relación entre 2 realidades distintas que aparecen y son, a la vez, «proporciones sagradas» desde el punto de vista esotérico, y números irracionales (de infinitos decimales), misteriosos aún en el aspecto más profano.
1 – EL NÚMERO Pi
Abordaremos en primer lugar sus aspectos más comunes, para tratar después de desvelar algunos elementos más sutiles de su misterio.
1a) – La notación π
π es la primera letra de la palabra griega perimetron, perímetro y perijereia, circunferencia, periferia. Hay muchas versiones sobre la aparición de este símbolo, pero la época parece ser siempre la misma. Fue alrededor de 1600 cuando los matemáticos y teólogos ingleses William Oughtred (1574-1660) e Isaac Barrow (1630-1677) y también el matemático alemán Ludolph van Ceulen (1539-1610) utilizaron el símbolo π para representar el perímetro de un círculo de diámetro 1.
1b) – La actualidad del número Pi: el cálculo decimal.
El pensamiento moderno ha experimentado una gran fascinación por el número Pi, pero no en su aspecto cualitativo, como se desarrolló en la antigüedad, en su naturaleza relacionante y en el sentido misterioso de esta relación (que estudiaremos después), sino en su aspecto cuantitativo, es decir, en el cálculo del decimal, que será ampliado en el Renacimiento con el desarrollo de las ciencias racionales.
Nos podemos encontrar, por ejemplo, todo un historial de la búsqueda de los decimales del número Pi desde la antigüedad hasta nuestros días. Si bien hay que remontarse a la época sumeria o egipcia para encontrar referencias geométricas al número Pi, es Arquímedes de Siracusa, físico y matemático griego de Sicilia, (en la magna Grecia), el que en el año 250 a.C comienza realmente a calcular los decimales del número Pi a través de la búsqueda de la cuadratura del círculo. Fue el primero que utilizó un algoritmo para el cálculo.
El método, al que normalmente se llama hoy en día el método de Arquímedes, consiste en calcular el perímetro de los polígonos regulares inscritos y circunscritos en un círculo, para encuadrar el perímetro del círculo y deducir un encuadramiento de Pi. Así obtuvo
3+10/71 < π < 3+1/7 = 22/7
En Europa podemos citar al italiano Fibonaci que, en 1220, encuentra el valor 3,141818. En los Países Bajos Van Ceulen calcula 34 decimales en 1609. Luego vino el desarrollo de técnicas para el análisis de los cálculos: Newton (16 decimales en 1665) y Machin (100 decimales en 1706), seguidos de Euler (20 decimales calculados en una hora en 1760) y muchos otros. Los hermanos Chudnovsky calcularon 4 mil millones de decimales en 1994; Kanada y Tamura 206 mil millones de decimales (en aproximadamente 33 horas de cálculos). Kanada batió su propio récord el 6 de diciembre de 2002 con un equipo de nueve investigadores japoneses: 1.241 mil millones de decimales fueron calculados con la ayuda de un superordenador Hitachi (en 400 horas de cálculos), mediante un algoritmo que el equipo tardó cinco años en poner a punto.
A partir del 31 de diciembre de 2009 ¡se conocen alrededor de 2700 mil millones de decimales del número pi! Podemos preguntarnos: ¿de qué sirve conocer tantos decimales de pi? El conocimiento de los decimales de pi es una prueba muy buena para comprobar la precisión de los cálculos de los ordenadores (dos graves errores fueron detectados así en los super-ordenadores IBM 590 y R8000). Sin embargo, la motivación más importante no es saber más y más decimales de Pi, sino más bien poder hacer cálculos; esto implica unos algoritmos de cálculos muy
elaborados.
Los 100 primeros decimales de pi: 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067.
Como anécdota, señalaremos que hoy en día existen unas jornadas anuales de aproximación al número Pi. Google ha elegido como el día anual de Pi el 14 de marzo (el 14 de marzo en los Estados Unidos es el 3/14 y su fiesta se celebra generalmente a la 1h.59, o sea, las 13h.59; para más coincidencia, el 14 de marzo es la fecha del aniversario de Einstein. En Francia hemos preferido el 22 de julio (22/7).
Google ha ideado un logo para la ocasión, que mostramos seguidamente.
En el Palacio del Descubrimiento en Paris existe la Sala del Número Pi, que se presenta con los 704 primeros decimales. Una serie de paneles resumen a grandes rasgos la historia de este número y algunos de los problemas relacionados con la aguja de Buffon, la cuadratura del círculo, etc…
1c) – ¿Qué es el número 
? Definiciones matemáticas
Todos conocemos la fórmula que nos da el perímetro de un círculo a partir de su diámetro o de su radio y del número que vale algo así como 3,1415926535… Perímetro de un círculo = x Diámetro de un círculo = x 2 x Radio de un círculo, de ahí la definición clásica de :
es la relación constante entre la longitud de un círculo (el perímetro) y su diámetro (el doble de su radio).
O bien, a partir de la fórmula que permite calcular el área (la «superficie») de una circunferencia. Área de una circunferencia = x (radio del círculo)²
es la relación constante entre el área de un círculo y el cuadrado de su radio.
Sin embargo, para el matemático las dos definiciones anteriores del perímetro del círculo o del área de la circunferencia suponen que el espacio euclidiano considerado por el informe «perímetro del círculo / diámetro» es constante e independiente del círculo elegido. Los matemáticos prefieren las definiciones basadas en el análisis, como ésta:
es el número real más pequeño p > 0 igual que cos (p) = -1
Otras definiciones matemáticas se desarrollan en esta visión analítica, pero no vamos a continuar con ellas.
1d) – La naturaleza algebraica de
Según las matemáticas modernas no es un número decimal, ya que las cifras después de la coma nunca terminan ( tiene infinidad de decimales).
es un número irracional: no se puede escribir como una fracción de dos números enteros. En otras palabras, significa también que las cifras de no son previsibles. No podemos imaginar un decimal sin la correspondiente calculadora. La irracionalidad de fue demostrada en 1761 por el alemán Lambert. es un número trascendente: no hay solución alguna con coeficientes racionales. Esto fue demostrado en 1881 por Lindemann.
1e) – ¿Cuál es la verdadera naturaleza de : la cuadratura del círculo
Para comprender la verdadera naturaleza de hay que ir hacia atrás en la historia y descubrir cómo fue utilizado este número por los antiguos para intentar resolver el problema de la cuadratura del círculo. La cuadratura del círculo fue uno de los grandes problemas de la geometría en la antigüedad y se ha mantenido a lo largo del tiempo. Consiste en construir con regla y compás un cuadrado con la misma área que un círculo de radio dado, lo cual nos lleva a construir el número (más exactamente la relación) que resulta igual a la raíz cuadrada de . ¿Es posible construir un círculo y un cuadrado de la misma área con una regla y un compás? ¿O construir igualmente un cuadrado y un círculo del mismo perímetro?
Esta pregunta, que parece simple, ha desafiado -sin embargo- a los matemáticos durante más de 34 siglos.
Desde 1650 a.C., o puede que incluso antes (aunque no tenemos constancia por escrito), los egipcios se interesaron por el tema. El escriba Ahmés, autor de un célebre papiro, nos ofrece una solución aproximada. Para él, la cuadratura del círculo es, sin duda, posible: es el cuadrado de lado 8d/9 donde d es el diámetro del círculo. Pero se equivoca.
La figura coloreada en rosa, ¿puede ser igual a la coloreada en violeta?
Mucho tiempo después de los egipcios y del geómetra Hipócrates de Quios (siglo V a.C), Arquímedes de Siracusa (287-212 A. C.) comenzó a interesarse por los objetos cuyo tamaño (longitud, área, volumen) podían tener algo que ver con los delcírculo (esfera, cilindro, cono, espiral) y propone una metodología de cálculo para abordar la medición de la circunferencia.
Por supuesto, uno puede aproximarse a la cuadratura del círculo. Y eso es lo que seguramente harían los científicos de los siglos siguientes. Tal como hizo Anaxágoras de Clazomene (500 a.C), primer científico griego que se interesó por esta cuestión. Posteriormente fue Nicolás de Cusa (1404-1464), erudito y famoso Cardenal, quien sostiene que 3,1423 es el valor exacto de Pi.
En 1685, un polaco, el padre Kochansky, construye una aproximación geométrica de Pi con un error de menos de 0,02 por mil. Al ser presentado como un número racional, es decir, un número que se expresa como una fracción, la cuadratura sigue pareciendo posible.
Fue en 1882 cuando el matemático alemán Ferdinand von Lindemann demostró la trascendencia de Pi. ¿Transcendencia? Esto significa que Pi no puede ser la solución de una ecuación algebraica de coeficientes enteros. No puede adaptarse a cualquier ecuación algebraica con coeficientes racionales. Se trata de una secuencia infinita de términos.
En otras palabras, no podemos representarla geométricamente: la cuadratura del círculo es imposible (al menos en su aspecto racional).
Hoy en día, este problema, no resuelto durante más de 3000 años, se ha integrado en el lenguaje actual, y decir «buscar la cuadratura del círculo» es una expresión que se refiere a «tratar de resolver» un problema que no tiene solución.
Vayamos más lejos: poner en relación el círculo y el cuadrado es buscar un vínculo concreto entre 2 realidades distintas: · El círculo simboliza la unidad primordial, lo absoluto, los poderes celestes, el infinito, representado en numerosas tradiciones por una unidad ternaria (el 0, el 1 y el 3).
· El cuadrado representa el mundo manifestado, concreto, la materia, con sus 4 elementos.
· El principal problema de la cuadratura del círculo es crear un puente: «de arriba abajo» o «de dentro afuera», es decir, a partir de la unidad (el círculo) y buscando encarnarla en la manifestación (el cuadrado), se puede pasar por la relación del círculo con su diámetro; la división de la unidad en pluralidad.
· En sentido inverso, llevar la materia (el cuadrado) al nivel del círculo, es «espiritualizarla»; esta opinión coincide con el proceso alquímico que busca elevar la materia para hacer emerger el espíritu, lo que es también un retorno a los orígenes.
Realizar la cuadratura del círculo es crear un vínculo con los orígenes, permitir el pasaje de lo sagrado a través de lo terrestre (el cuadrado) y lo celeste (el círculo); en la Edad Media, la cuadratura del círculo se percibía como un saber secreto que daba acceso a lo divino. Ahora podemos comprender mejor el aspecto «trascendente» de destacado por los matemáticos modernos; o también el aspecto irracional que le confiere una dimensión que no se puede integrar en el plano concreto de la manifestación. Más que intentar medirla, nosotros podemos vivirla; esto es lo que buscaban los filósofos de la antigüedad, conectando la filosofía con el mundo de las causas; Pitágoras llegó a decir en cierta ocasión que «Dios geometriza».
Durante largo tiempo, la geometría ocupó un lugar privilegiado en la enseñanzade las matemáticas. Geometría viene del griego «geos», tierra, y «metros», medida. Es por tanto la ciencia de la medición de la tierra. Es sin duda en el antiguo Egipto donde se sitúa el origen de esta disciplina, cuando las inundaciones periódicas del Nilo destruían las parcelas de los agricultores con la crecida. Gracias a esta ciencia se podían restablecer de nuevo las lindes, permitiendo volver a distribuir los terrenos a los campesinos, una vez que el río recuperaba su cauce.
Los egipcios crearon una cuerda con 12 nudos colocados a distancias iguales, con la que trazaron, tensándola a partir de un ángulo recto, el triángulo 3, 4, 5 (llamado 10 más tarde triángulo de Pitágoras). Como es natural, este conocimiento se exportó a Grecia siendo muy bien recibido y aceptado desde entonces. Hay que destacar 2 filósofos y sabios griegos presocráticos, célebres por haber practicado y enseñado la geometría:
Tales de Mileto (625-547 a.C), fue uno de los Siete Sabios de Grecia y el fundador de la Escuela de Mileto. Él pudo medir las pirámides de Egipto calculando la relación entre su sombra y la de nuestro cuerpo, relacionando así a Egipto con la geometría.
Pitágoras fue también a aprender a Egipto siguiendo la trayectoria iniciada por Tales; él trajo la famosa estrella pentagrama, o estrella de cinco puntas, emblema de su Escuela Pitagórica, y símbolo vinculado fuertemente a la enseñanza del Número de Oro.
En la filosofía pitagórica, la geometría ocupa un lugar especial, porque permite establecer relaciones con los números, principios de todas las cosas visibles, y plasmarlos a través de figuras en el espacio, lo que permite el desarrollo de la intuición en contacto con lo divino… (la geometría fue utilizada en astronomía como un vínculo entre la tierra y las estrellas).
1f) – Algunos ejemplos en la historia de la cuadratura del círculo, racionalmente imposible como hemos visto, pero que es posible vivir interiormente
La relación del cuadrado con el círculo o del diámetro con su círculo era simbolizada en la antigüedad por las letras I y O como representación de la búsqueda de la unidad, del retorno a los orígenes, que dieron lugar en la Escuela Pitagórica a los ritmos y al canto de las vocales.
En China, en los antiguos textos del Tao, se contaba: «El cielo es una esfera, la tierra es un cuadrado». En Pequín, la ciudad prohibida, la sede y el símbolo del poder se estructuró con el cuadrado, mientras que el palacio del cielo, simbolizando la espiritualidad y lo divino, estaba constituido por tres monumentos circulares.
La mayoría de nuestros edificios religiosos tienen un suelo de baldosas cuadradas y se elevan en arcos circulares, realizando así un vínculo (religión viene de religare, que significa religar) entre la tierra y el cielo. En La Meca, los peregrinos efectúan un paseo circular alrededor del cubo de la Kaaba. A través de este acto de fe, el Islam realiza espiritualmente la cuadratura del círculo.
En la India, en los diseños de los mandalas para la meditación, se pueden ver el círculo y el cuadrado asociados. Ellos representan la armonía ideal de los pares de opuestos, el cielo y la tierra, lo divino y lo humano.
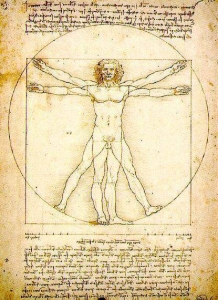
En el Hombre de Vitrubio de Leonardo de Vinci, encontramos al hombre de proporciones ideales situado entre el cuadrado y el círculo.
1g) – Las Enseñanzas Esotéricas
En el volumen I de La Doctrina Secreta (que trata de la cosmogénesis) según las enseñanzas esotéricas, H.P. Blavatsky aporta un significado más profundo. Ella distingue el número Uno sin segundo (la Unidad Primordial) representado por el círculo, del número Uno con segundo (la Unidad portadora de la multiplicidad potencial con los números 1, 2 y 3) generando las etapas de la creación del mundo.
El número Pi interviene como la transición entre el mundo precósmico y el mundo manifestado con el número 4, simbolizado por el cuadrado que conocemos. Por el número Pi, las cosas son objetivas. Inversamente, desde el mundo manifestado, el número Pi es percibido como «la Puerta de los Misterios», que da acceso al mundo invisible, sin forma.
2 – EL NÚMERO DE ORO o “LA DIVINA PROPORCIÓN”
El Número de Oro también ha fascinado a los seres humanos desde la más remota antigüedad, y podemos encontrarlo en numerosas construcciones a lo largo de la historia. Está también presente en la Naturaleza y por lo tanto en el ser humano, lo cual explica que le «acompaña», ya sea consciente o inconscientemente, en todas sus obras. Se le podrían aplicar muchos nombres como símbolo de la armonía universal: fue llamado «el número de la creación», «el número de Dios», «la divina proporción», ya que este número se define ante todo como una cierta relación.
Se le designa por la letra griega ( phi ) en homenaje al escultor griego Phidias (s. V a.C.) cuyos frisos decoraban el Partenón de Atenas.
2a) – Breve historia de la presencia del Número de Oro en distintas obras y monumentos
2800 a. C.: La pirámide de Kéops tiene una dimensiones que resaltan la importancia que su arquitecto daba al número de oro. Según Herodoto, los sacerdotes egipcios decían que las dimensiones de la Gran Pirámide habían sido elegidas de forma que «El cuadrado de la altura vertical equivalía exactamente a la superficie de cada una de las caras triangulares».
En el s.V a.C. (447-432 a.C.) el escultor griego Fidias utiliza el número de oro para decorar el Partenón de Atenas, y en particular para esculpir la estatua de Atenea Partenos. Utiliza igualmente la raíz cuadrada de 5 como referencia.
Platón define en el paradigma de la línea cuatro grados de conocimiento (sombras, objetos, conceptos e ideas), que conectan el mundo sensible con el mundo inteligible, cuyos planos están separados entre sí por relaciones áuricas (La República – libro IV).
El teatro de Epidauro contiene dos series de gradas, una de 21 y otra de 34, dos números consecutivos de la serie de Fibonacci cuya relación está cercana al número de oro.
En el s. III a.C. Euclides evoca el intercambio de un segmento en «media y extrema razón» en el libro VI de los Elementos.
En la Edad Media, los constructores de catedrales, haciéndose eco de las antiguas tradiciones milenarias en el arte de la construcción de templos, nos
transmitieron las medidas en relación con el cuerpo humano: la palma, la aleta (los dedos), el empalme, el pie y el codo.
Esto produce dos resultados sorprendentes: pasar de una medida a otra multiplicando por el número de oro 
·la aleta = la palma x
·el pie = el palmo x
·el codo = el pie x
Una unidad de medida es igual a la suma de las dos precedentes
·palmo = palma + aleta
·pie = palmo + aleta
·codo = palmo + pie
5 unidades de medida relativas al cuerpo humano:
la palma = 34 líneas = 7,64 cm = 1/²
la aleta = 55 líneas = 12,36 cm = 1/
el palmo = 89 líneas = 20 cm = 1
el pie = 144 líneas = 32,36 cm =
el codo = 233 líneas = 52,36 cm= ²
Con una unidad de base: la línea = 2,247 mm.
En 1498 Fray Luca Pacioli, un monje profesor de matemáticas, escribió «La divina proporción» ilustrado por Leonardo de Vinci. La divina proporción fue utilizada por los artistas del Renacimiento en sus cuadros.
El hombre de Vitruvio – 1490 – Leonardo de Vinci. Al colocar un hombre en el interior de dos figuras geométricas perfectas, el cuadrado y el círculo, Leonardo de Vinci demuestra que las proporciones del cuerpo humano responden a una perfecta armonía.
En el s. XIX: Adolf Zeising (1810-1876), doctor en filosofía, profesor en Leipzig y después en Munich, habla de la «Sección Aúrea» y no se interesa por la geometría sino en lo concerniente a la estética y a la arquitectura. Él fue el que introdujo el lado mítico y místico del número de oro.
Al principio del s. XX: Matila Ghyka, diplomático rumano, se basó en los trabajos del filósofo alemán Zeising y del físico alemán Gustav Theodor Fechner; sus
obras La estética de las proporciones en la naturaleza y en las artes (1927) y El Número de oro. Ritos y ritmos pitagóricos en el desarrollo de la civilización occidental (1931) insisten en la importancia de este número. A lo largo del s. XX: pintores como Dali y Picasso, y también arquitectos como Le Corbusier, recurrieron al número de oro.
El número de oro ha sido verdaderamente un pequeño nirvana aritmético para tener una visión privilegiada de la comunicación con el más allá… En 1945 Le Corbusier patentó su Modulor, un sistema que relaciona matemáticamente las proporciones entre las diferentes partes del cuerpo humano y la arquitectura.
2b) – Definición y valor del número de oro
La primera definición conocida es sin duda la de Euclides en Elementos, libro VI, 3ª edición: «Una línea se dice que está dividida en extrema y media razón cuando toda ella es al segmento mayor lo que éste es al segmento menor».
Definición un poco compleja que se puede traducir más claramente como «elmás pequeño (segmento) es al más grande, lo que el más grande es al todo». De esta manera queda establecida la relación entre lo más pequeño y el Todo. Aquí hemos expresado el principio fundamental de cualquier edificio religioso. La divina proporción que existe entre lo más pequeño, lo más grande y el Todo es tal, que lo pequeño (el microcosmos, el hombre) se encuentra «naturalmente» en relación con el Todo (el macrocosmos, el universo), lo Divino. Esto requiere que lo más grande (el Templo) sea diseñado y realizado como un mesocosmos, es decir, un espacio intermedio, que canaliza las leyes de la Naturaleza.
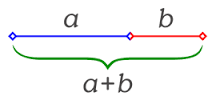
si b = el más pequeño (segmento)
a = el más grande;
a+b = el Todo
Ahora b/a = a/a+b lo que nos da: a/b = a+b/a =
o la ecuación:
= 1 + 1/ o también ²- -1 = 0
Es exactamente = 1+raiz cuadrada de 5 sobre 2
Phi = 1,618033988749895… pero con muchas propiedades matemáticas poco comunes.
De la ecuación anterior se deducen dos propiedades interesantes del número de oro
1- 2-1=
2- 1 sobre=-1
= > Es el único número que, al sumarle la unidad, se convierte en su cuadrado, y cuando se le sustrae la unidad el resultado es inverso
Por otra parte, los poderes del número de oro expresados en función de Phi y de1 y los coeficientes no son otros que los números de la serie de Fibonacci. Es entonces a
través de la geometría como el número de oro encuentra su sitio y su función.
2d) – Construcción geométrica del número de oro
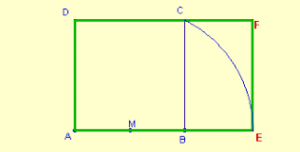
El rectángulo ABEF se llama rectángulo de oro, ya que sus lados tienen la proporción áurica.
• Tenemos el cuadrado ABCD
• Marcamos el centro de AD
• Hacemos un arco con centro en O y
trazamos la línea OC ; prolongamos AD a F
AF/AB representa una dorada proporción
CD/DF es también una dorada proporción
Cálculo:
Si definimos AD=AB=BC= 1 – OD = 1/2 y
OC² = OD² + CD² = + 1= 5/4
AF= AD+DF= =
CD/DF= 1/ f-1 =
La fascinación que posee por sí mismo el número de oro es de alguna manera recurrente y comunicativa, como si se tratara de un objeto geométrico que poseyera la propiedad de generar por sí mismo formas áuricas; es una suerte de propiedad estética que es contagiosa.
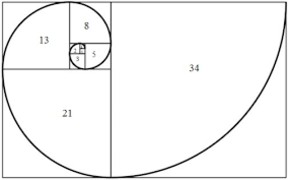
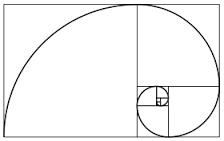
La Espiral de Oro
Esta espiral reproduce una sucesión de rectángulos de oro, alternativamente horizontales y verticales, a partir de un cuadrado y de un rectángulo de oro asociado.
Esto le da dos sentidos a la espiral de oro: uno ascendente (centrífugo) hacia lo infinitamente grande, y otro centrípeto hacia lo infinitamente pequeño.
2e) – La serie de Fibonacci
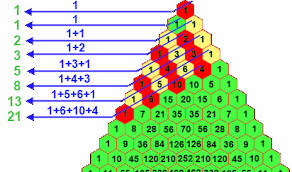
Fibonacci nació en Pisa en 1175 y fue uno de los grandes matemáticos de la Edad Media. Recogió en Argelia el conocimiento de los números árabes y, sobre todo, nos dejó la serie de cifras que llevan su nombre. El problema que utilizó y que ha inspirado a otros muchos matemáticos es el problema de los conejos: « ¿Cuántas parejas de conejos obtendremos al final de cada mes si comenzamos por una pareja y cada pareja produce cada mes una nueva, la cual se vuelve productiva también al segundo mes de su existencia ? » Este problema dio lugar a la serie de FIBONACCI : 1 ; 1 ; 2 ; 3 ; 5 ; 8 ; 13 ; 21 ; 34 ; 55 ; 89 ; 144 ; 233 ; 377 ;.. Cada término es la suma de los dos términos que le preceden.
La serie de Fibonacci
0 1 2 3 4 5 6 7 8 9 3 1 4
Examinemos la relación de 2 términos consecutivos de esta serie de Fibonacci:
F2 / F1 = 1 < F6 / F5 = 1,600 <
F3 / F2 = 2 > F7 / F6 = 1,625 >
F4 / F3 = 1,5 < F8 / F7 = 1,615 <
F5 / F4 = 1,666 > F9 / F8 = 1,619 >
Hay que tener en cuenta que la relación de dos términos consecutivos Fn / Fn-1 es alternativamente inferior y superior al número de oro. Esta información aborda el número de oro cuando el rango de los términos tiende al infinito:
Los lados de los cuadrados son los de la serie de Fibonacci 1, 1, 2, 3, 5, 8, 13 ..
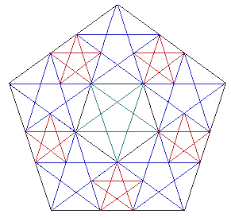
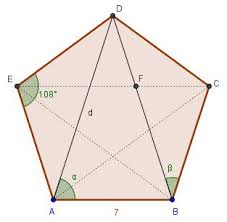
Triángulo de oro:
también es posible formar triángulos con medidas áuricas (aquí AB/BD = )
Los triángulos de oro se inscriben en un pentágono regular. La diagonal tiene una longitud de f=(1+v5)/2
El pentágono se recrea hasta el infinito con las medidas áuricas
2f) El Número de Oro, Perspectivas y Estética
La sucesión de números de Fibonacci nos da las claves de la perspectiva en un cuadro que se basa en el infinito.
Por ejemplo, la regla de los tercios (versión simplificada de la regla de oro) se utiliza a menudo en pintura o en el diseño para destacar algún tema en particular dentro de un cuadro. Consiste en dividir mentalmente el cuadro en 3 bandas verticales y 3 horizontales imaginarias; por razones de percepción estética, el tema ocupará el lugar «natural» sobre estas líneas, preferiblemente en la intersección de dos de ellas.
Esta proporción relacionada con la serie de Fibonacci o con el número de oro ha sido utilizada con frecuencia para lograr la armonía en las obras de arte, la arquitectura, la composición, el espacio y en la misma música.
Numerosos artistas han basado sus trabajos en marcos geométricos. Las proporciones áuricas aparecen siempre como las medidas más armoniosas e intuitivamente perceptibles.
2g) – Phi aparece a lo largo de la vida en todo el universo
El número de oro es una proporción. Lo destacable de esta proporción es que se encuentra en la mineral, vegetal, animal y humana; es una característica de la Vida.
He aquí algunos ejemplos.
El Número de Oro en el reino vegetal
Se pueden observar espirales en muchas plantas, como por ejemplo en los corazones del girasol, en la corteza de la piña tropical o también en la de las piñas de los pinos. La serie de Fibonacci y el Ángulo de Oro se encuentran en estas espirales.
Ejemplo: Una flor de girasol está constituida por dos grupos de espirales. Varios investigadores han demostrado así el crecimiento de las plantas
utilizando la informática en los experimentos de laboratorio.
Según los investigadores, la aparición de las espirales está basada en el ángulo de oro igual a 360°/(1+phi)=137,5°. El crecimiento de las plantas forma dos series de espirales que giran en direcciones contrarias.
El número de espirales en cada caso corresponde a dos términos consecutivos de la serie de FIBONACCI. Por ejemplo (13; 21) o (34;55) o (55;89) o (89;144).
El Número de Oro en el reino animal
La figura descrita por las conchas de algunos caracoles es una espiral de oro.
La proporción áurica es evidente también en algunos animales marinos, como las estrellas de mar o los erizos, cuyas formas recuerdan a la estrella del pentágono regular.
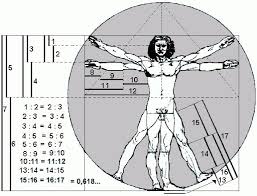
Ya hemos mostrado algunas proporciones a nivel de la mano por ejemplo. Todo cuerpo humano normalmente constituido comprende 1 cabeza, 2
manos, cada mano con 5 dedos y cada dedo con 3 falanges, excepto el pulgar que contiene 2. Tenemos aquí los números de Fibonacci. Numerosas
relaciones áuricas se pueden ver a simple vista, desde los brazos y a lo largo de todo el cuerpo.
Otra manifestación igualmente sorprendente del número de oro en el ser humano es que, si consideramos una línea recta desde la cabeza a los pies, pasando por el ombligo, el punto del ombligo divide el segmento según la regla de oro. Dicho de otra manera, el ombligo divide el cuerpo humano según la sección áurea. El cuerpo humano está hecho con proporciones divinas.
La espiral del ADN es una sección de oro. La molécula del ADN, el programa que tenemos para toda la vida, está basada en la sección áurea. Mide 34 angströms de ancho por 21 de largo para cada ciclo completo de su espiral de doble hélice. Las espirales del ADN están relacionadas con el número phi.
34 y 21, naturalmente, son los números de la serie de Fibonacci y su relación 1,6190476 se aproxima estrechamente a phi, 1,6180339.
Conclusión
Tanto el Número de Oro como el número Pi son mucho más que una simple curiosidad matemática desafiando nuestro intelecto. Son principalmente una serie de medidas y de relaciones entre dos realidades distintas que nuestra conciencia ordinaria trata de aprehender.
La proporción áurica es una característica de la Vida manifestada en nosotros mismos, en tanto que somos como un microcosmos en medio de un macrocosmos. Esto vincula lo infinitamente grande con lo infinitamente pequeño y viceversa.
El número Pi expresa a través de la cuadratura del círculo la misteriosa relación que existe entre el mundo de los orígenes, sin forma (arrupa), y el mundo manifestado (rupa), la relación entre la unidad y la multiplicidad. Estos dos opuestos, aparentemente irreconciliables, los podemos llegar a integrar en nuestro interior.
Podemos entender ahora por qué los antiguos pudieron utilizar la Geometría y la Música, las ciencias por excelencia, para expresar las medidas como parte de los misterios.
Un poema para recordar
Existen muchos poemas que se han escrito como medios mnemotécnicos para aprenderse los decimales en las distintas lenguas contando el número de letras de cada palabra.
La longitud de cada palabra da una cifra decimal (una palabra de 10 letras nos daría un código cero). La puntuación no aporta nada; he aquí uno que se puede aprender en los bancos de la escuela.
¡Me gusta aprender los números útiles a los sabios! 3 1 4 1 5 9 2 6 5 3 5
Immortal Arquímedes, artista ingeniero, 8 9 7 9
¿Puede tu decisión apreciar el valor? 3 2 3 8 4 6 2 6
Para mí, tu problema era de tales beneficios. 4 3 3 8 3 2 7 9
Antiguo, misterioso, un problema de bloqueo 5 0 2 8 8
Método admirable, una obra grandiosa 4 1 9 7 1 6 9
Que Pitágoras descubrió a los antiguos griegos 3 9 9 3 7 5
¡Oh cuadratura ! Viejo tormento para el filósofo 1 0 5 8 2 9
Insoluble redondez, que largo tiempo estuvo 9 7 4 9 4 4
Desafiando a Pitágoras y a sus seguidores. 5 9 2 3 0
¿Cómo integrar el espacio en un círculo, 7 8 1 6 4 0
Formar un triángulo que sea equivalente ? 6 2 8 6 2 0
Arquímedes descubrirá algo nuevo 8 9 9 8
Apreciará en el espacio de un hexágono 6 2 8 0 3 4
Fuentes y bibliografía
Doctrine Secrète – Tome 1 – HPB – édition Adyar
Symbolique des cathédrales – F Schwarz- édition du 8° jour
Qu’est ce que la Philosophie Antique ? – Pierre Hadot – édition Folio
Géométrie du nombre d’or – Robert Vincent éditions Chalagam
Le nombre d’Or Matila Ghyka – éditions Gallimard
Le Nombre d’Or, clé du monde vivant – D. Neroman – Dervy livres
Numéro spécial , Supplément au Petit Archimède no 64-65, mai 1980
Le fascinant nombre , Jean Paul Delahaye, Éditions Belin, Pour la Science
Autour du nombre Pi, Pierre Eymard, Jean-Pierre Lafon, Éditions Hermann,
Paris, 1999 –
À la poursuite de , Jörg Arndt & Christoph Haenel : Éditions Vuibert, 2006
wikipedia et encyclopédie universalis